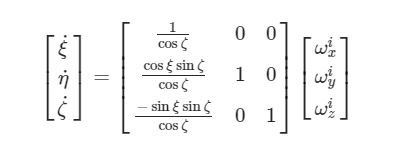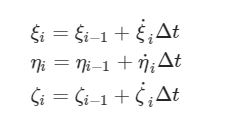Orientiamoci! Determinare l’orientamento di un oggetto (parte 1)

In questa serie di articoli (qui il secondo) spiegheremo come si realizzano dei semplici sistemi che permettano di determinare l’orientamento nello spazio di un oggetto, che è alla base dei moderni sistemi di motion capture utilizzati nell’industria videoludica e cinematografica d’animazione. Gli stessi principi vengono utilizzati in aeronautica per stabilire l’orientamento dei velivoli.

Nel primo articolo ci limiteremo a comprendere la matematica che sta dietro il calcolo dell’orientamento di un corpo, mentre nel secondo imposteremo un semplice codice C++ per applicare la matematica qui esposta tramite una scheda Arduino.

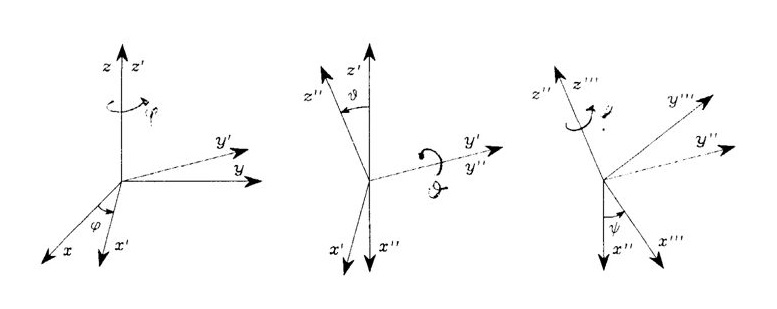
Angoli di Eulero. Servono a descrivere l’orientamento di un corpo nello spazio.

L’idea di base

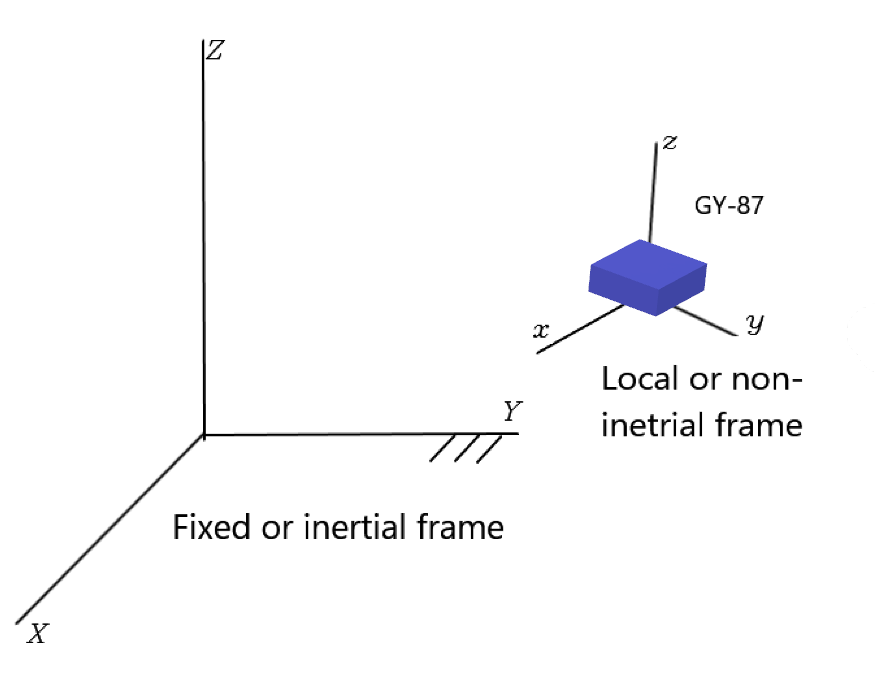
Per sapere come un qualsiasi corpo sia orientato nello spazio è necessario stabilire un set di parametri opportuno e conoscerne il valore in ogni istante. Comunemente si utilizzano gli angoli di rollio, beccheggio e imbardata, definiti come in figura. Non sono necessarie altre informazioni come ad esempio posizione, velocità ecc. perché queste ultime e gli angoli sopracitati possono essere rilevate indipendentemente, anche se dovesse esistere una qualche relazione tra di loro.

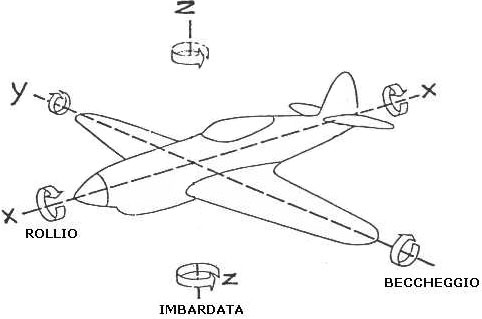
Angoli di un corpo.

Rollio, beccheggio e imbardata sono i nomi che vengono comunemente dati ad una particolare terna di angoli, che vengono chiamati angoli di Eulero. Questi, come vedremo più avanti, si possono indicare in generale, anche come angoli di Cardano.

Un po’ di matematica

Nel seguito si farà riferimento agli angoli definiti nella figura sottostante.

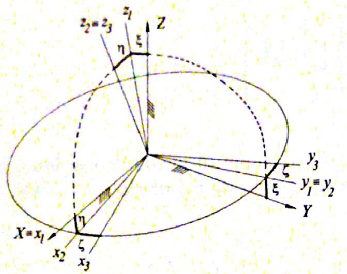
Angoli di Cardano con relativi assi.

Gli angoli di Cardano descrivono l’ampiezza delle rotazioni attorno ai tre assi relativi al corpo di cui si vuole conoscere l’orientazione. Queste rotazioni formeranno degli angoli tra il sistema di riferimento del corpo e quello assoluto; il primo viene detto anche sistema mobile, il secondo fisso. I due sistemi di riferimento devono avere l’origine degli assi in comune.

Sono quindi definiti gli angoli:

Le rotazioni che possono essere descritte da questa terna possono essere associate ad una matrice detta appunto matrice di rotazione. Considerando separatamente i tre angoli, quindi, si possono scrivere le seguenti:

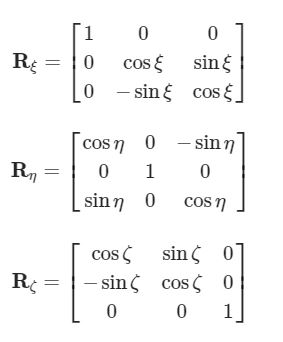
Per descrivere una rotazione completa si devono premoltiplicare le matrici tra loro: questo rende il risultato ovviamente non univoco. Esistono sei possibili combinazioni di queste matrici. Quella che verrà utilizzata è la seguente:

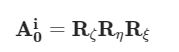
Questa combinazione è quella che fornisce agli angoli il nome di angoli di Eulero. La matrice che ne risulta è:

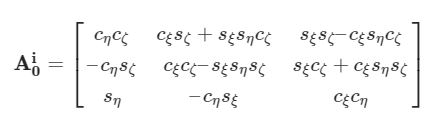
Sarà utile anche la sua inversa:

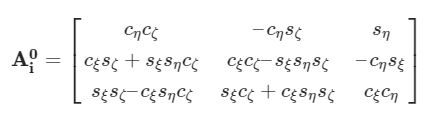
dove ovviamente c=cos, s=sin.

Perché servono queste matrici?

E’ possibile notare che le matrici presentano un pedice e un apice, rispettivamente 0 e i. Questo perché si relazionano le quantità che vengono calcolate e/o misurate nel sistema di riferimento fisso, con le analoghe nel sistema di riferimento mobile, e viceversa.

In particolare, la prima permette di passare dal sistema di riferimento fisso a quello mobile; la seconda da quello mobile a quello fisso.

Risvolto pratico

La possibilità di esprimere “informazioni” analoghe in due sistemi di riferimento risulta particolarmente utile nel problema della determinazione dell’orientamento.
Di un corpo od oggetto è possibile conoscere, grazie a dispositivi appositi, le accelerazioni e le velocità di rotazione. I sensori che le rilevano sono rispettivamente accelerometro e giroscopio.

E’ diffusa la convinzione che la velocità angolare sia la derivata dell’angolo di rotazione di un corpo. Essendo anche la quantità che viene misurata da un giroscopio, molti makers “prendono” il segnale proveniente dallo stesso e procedono all’integrazione, ritenendo così di ottenere l’orientamento di un oggetto.

Tuttavia, il fatto che la velocità angolare sia la derivata dell’angolo non è assolutamente vero in quanto questa, come dimostreremo a fine articolo, non è il differenziale di alcun vettore e quindi non può essere integrata. E’ invece vero che il modulo della velocità angolare si può esprimere nel seguente modo:

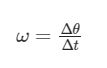
non è possibile conoscere altro tramite questa operazione che non è una derivazione, ma un tasso di variazione.

Gli angoli di Cardano sono stati introdotti anche perché, a differenza delle velocità angolari, sono derivabili e sono quindi le quantità che consentono di ottenere tramite integrazione l’orientamento di un corpo.

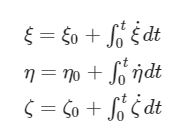
Algoritmo di calcolo

Nel sistema di riferimento mobile, cioè quello solidale con l’oggetto, si conoscono sempre le velocità angolari (tramite il giroscopio); in quello fisso le velocità angolari vanno a coincidere con le derivate degli angoli di Cardano. E’ quindi naturale pensare ad un algoritmo che sfrutti la conoscenza delle ω e degli angoli per ricavare l’orientamento.

Si può procedere sfruttando le due matrici di rotazione introdotte precedentemente. L’algoritmo verrà impostato in questo modo:

1. ottenimento dei dati di velocità angolare tramite giroscopio;
2. trasformazione delle velocità angolari nelle derivate degli angoli di Cardano con la matrice inversa;
3. integrazione per ottenere gli angoli di Eulero.

Come si potrà notare facilmente a breve, questo algoritmo risulta essere di tipo iterativo: si useranno i risultati del passaggio precedente per ottenere i dati richiesti nel passaggio corrente.

In termini matematici, detta i l’iterazione corrente e i-1 l’iterazione precedente i come apice delle ω indica il riferimento mobile):

1. 1. ottenimento delle derivate degli angoli di Cardano:

      

   2. integrazione degli angoli

      

   3. nuova iterazione con i risultati appena ottenuti.

Per l’iterazione i=1 serviranno i valori degli angoli per i=0 per poter procedere con l’integrazione. Come vedremo nel prossimo articolo, il valore degli angoli i=0 può essere ricavato in maniera ottimale anziché arbitraria, la quale sarebbe la soluzione più semplice.

Bonus: non integrabilità della velocità angolare

Per una trattazione più completa si rimanda al riferimento 1.

Un esempio

Non è facile fornire una spiegazione semplice del perché la velocità angolare non sia integrabile., ma può essere intuibile con il seguente esempio: se una persona seduta su una sedia da ufficio si mette a girare su se stessa, può capire di quanto ha ruotato solo se tiene gli occhi aperti. Se questa tiene gli occhi sempre chiusi risulterà estremamente difficile determinare con precisione la rotazione compiuta.
Integrare il segnale del giroscopio, cioè la velocità angolare nel sistema mobile, “corrisponde a ruotare con gli occhi chiusi”: nel prossimo articolo sarà mostrato come questo approccio porti a dei risultati totalmente sbagliati.

Questo esempio non è comunque sufficiente a dimostrare l’asserto di questo paragrafo, per cui si procede con la dimostrazione matematica.

Dimostrazione

Come da riferimento 1, le velocità angolari si possono esprimere in funzione degli angoli di Cardano:

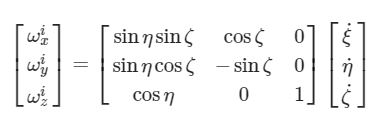
Si può esprimere allora la componente ad esempio, come:

Esprimendola come differenziale, si ottiene:

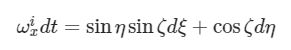
Come è noto, un differenziale

è integrabile se e solo se vale la condizione

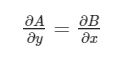
Si ricava che la velocità angolare non è integrabile (ripetendo gli stessi passaggi anche per le altre componenti) visto che

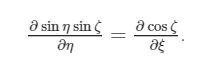
Per quanto riguarda le derivate degli angoli di Cardano si è visto che vale la seguente:

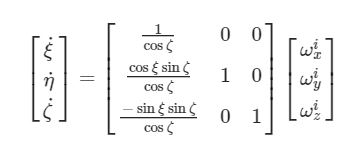
per cui, esprimendo la componente ξ come differenziale:

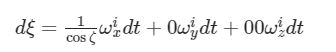
si vede che vale la condizione di differenziabilità, dato che

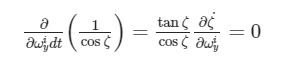
in quanto è facile vedere cheche è uguale alle altre componenti del differenziale.
Ripetendo per le altre componenti questi passaggi, si dimostra l’asserto.

Riferimenti

1. Cinematica e dinamica dei sistemi multibody, vol.2 (Ettore Pennestri’, Federico Cheli; 2009 Casa editrice Ambrosiana)
2. Elementi di Fisica, meccanica e termodinamica (Mazzoldi, Nigro, Voci; 2007)

Salvatore Campolo

Laureato in Ingegneria Meccanica, appassionato di motori e musica. Mi piace scoprire la ragione scientifica delle cose.