Le sospensioni: cosa sono e cosa fanno (parte 2)
Il focus di questo secondo articolo sarà posto sulla impostazione cinematica delle sospensioni di un autoveicolo.
Che cos’è l’impostazione cinematica
Per impostazione cinematica delle sospensioni si intende quel processo col quale si impone il comportamento del gruppo ruota. Lo studio si compie andando a ricercare i cosiddetti gradienti cinematici, relazioni che legano due traslazioni e tre rotazioni del veicolo allo spostamento verticale. In questo modo vengono riportati i moti espressi nel riferimento del veicolo, visibile nella figura in basso, in un vettore velocità e rotazione posizionati sull’asse di sospensione. Scopo della ricerca dei gradienti cinematici è la disposizione di questo asse nello spazio; questa posizione può essere qualsiasi.
Con riferimento alla figura in basso, si identificano quindi i seguenti moti:
- traslazione longitudinale x;
- traslazione trasversale y;
- rollio

- beccheggio

- imbardata

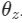
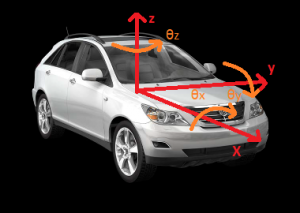

Sistema di riferimento del veicolo centrato nel baricentro.
La relazione tra le varie grandezze è la seguente
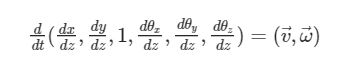
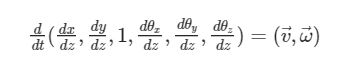
ed esprime quindi, in forma matematica, il legame ricercato. Le derivate rispetto a z dei diversi moti sono quindi le espressioni da definire per poter trovare i vettori v e θ.
Come si definiscono i gradienti
Per poter dare una definizione operativa delle derivate della formula precedente si cerca di esprimere le derivate della formula precedente con delle quantità misurabili, rilevate dalla geometria del gruppo sospensione.
Convergenza
Con convergenza si intende l’angolo formato tra la mezzeria lungo x del veicolo e la mezzeria della ruota. Visto dall’alto, l’angolo di convergenza ε è positivo quando le ruote puntano verso l’interno dell’auto. Senza entrare nel dettaglio, poiché non è obiettivo di questo articolo, l’angolo di convergenza va a modificare istante per istante il valore di forza laterale trasmessa a terra dagli pneumatici. Si intuisce come un valore negativo migliori l’inserimento e la trazione in curva e di solito si impiega nelle auto sportive, mentre per le auto stradali si preferisca un valore positivo per favorire un comportamento sottosterzante del veicolo.
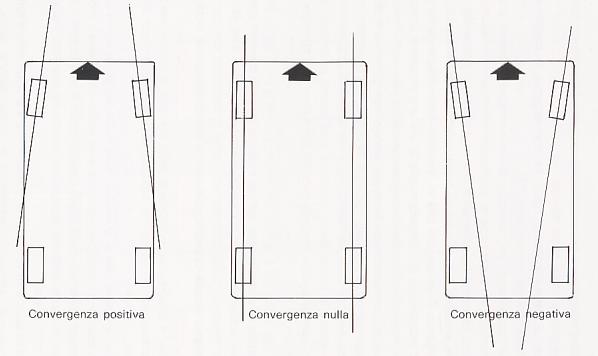

Normalmente, si può esprimere la convergenza con una funzione del tipo ![]()
![]()
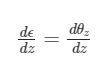
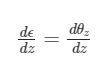
che indica in che misura lo pneumatico ruota attorno all’asse z del veicolo quando viene imposto uno spostamento verticale.
Altezza del centro di rollio
Il centro di rollio, o meglio l’asse di rollio (su ogni sezione trasversale del veicolo è possibile infatti trovare questo punto) è definito come il luogo attorno al quale il veicolo e la massa non sospesa ruotano se soggetti ad un’azione di inerzia in curva. La posizione di questo luogo modifica il comportamento dello pneumatico nella direzione laterale, cioè y. Si individua sulla verticale del veicolo una volta che viene eseguita la costruzione in figura seguente.
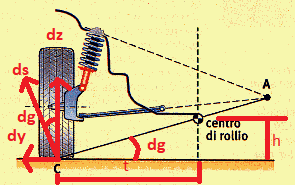

Individuazione del centro di rollio per una sospensione Mc Pherson.
Quando il veicolo entra in curva, lo pneumatico ruota della quantità ds, che ha le componenti in figura orientate secondo il sistema di riferimento consueto. Per l’angolo dg che si forma tra queste due componenti vale![]()
![]()
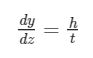
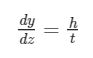
e quindi è possibile prevedere lo spostamento laterale dello pneumatico quando c’è uno spostamento verticale come rapporto tra altezza del centro di rollio h e semi carreggiata del veicolo t.
Anti-dive e anti-lift
Questi due termini indicano due comportamenti dovuti alla dinamica longitudinale dell’auto in accelerazione e frenata. L’anti-dive indica la tendenza dell’auto ad opporsi al “puntare in avanti” in frenata, mentre l’anti-lift indica la capacità dell’auto di opporsi all'”impennata” quando si accelera da fermi. La combinazione di questi due termini consente di trovare altri due gradienti cinematici.
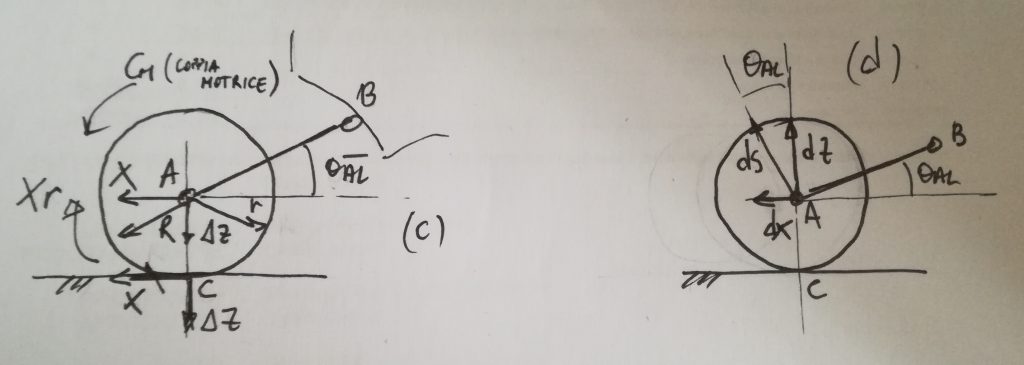
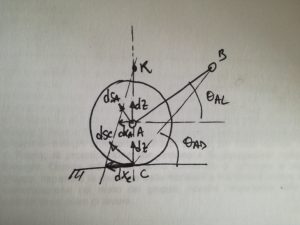
SI immagini che la ruota anteriore di un veicolo sia collegata alla cassa tramite un singolo braccio, come in figura. In frenata la forza X è diretta in direzione opposta al moto e vi sarà un trasferimento di carico che provoca un aumento della forza Z, ΔZ, tra pneumatico e terreno. La risultante R sarà inclinata rispetto al suolo dell’angolo ![]()
![]()
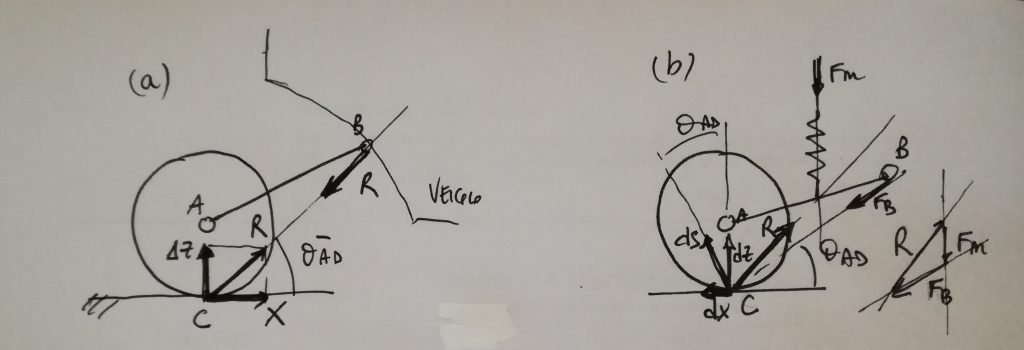

Nella situazione (a), se la cerniera B del braccetto è passante per il centro di beccheggio (definizione analoga a quella del centro di rollio), l’auto non si inclinerà in avanti poiché il sistema è in equilibrio. Questa viene detta condizione di Anti-dive 100%. E’ però una condizione svantaggiosa, in quanto tutta la forza R si scarica sulla cassa generando vibrazioni e sollecitazioni eccessive. Ci si “accontenta” allora di avere una situazione come in (b) dove, consentendo una traslazione lungo x dello pneumatico quando si applica lo spostamento z, si può scaricare parte della R sulla molla. Questo genererà un’inclinazione del veicolo in avanti.
Matematicamente, le forze X che si generano in frenata sono diverse tra assale posteriore ed anteriore a causa della ripartizione di frenata p (2). La loro espressione, estremamente semplificata, si può scrivere come una funzione della massa m e dell’accelerazione del veicolo, nonché della ripartizione
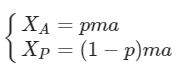
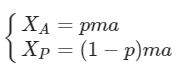
Le forze verticali Z, come si vede in (2), hanno invece la seguente espressione
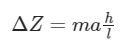
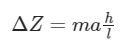
dove h è l’altezza del baricentro ed l il passo del veicolo. Dalla (a) si trova allora che
![]()
![]()
dove con AD si è indicato un valore compreso tra 0 e 1 corrispondente alla percentuale di anti-dive desiderata. Da (b) si ricava allora che
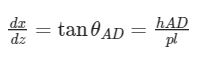
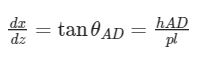
Per l’anti-lift si fa una trattazione analoga, ma anziché considerare l’angolo tra il terreno e la direzione della reazione R, si considera quello tra terreno (con una linea parallela ad esso passante per il centro ruota) e il braccio che collega centro ruota e cerniera B.

In questo caso scompare il termine p, e si ottiene un’espressione simile
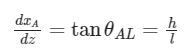
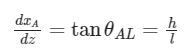
Come si vede dalla figura successiva, l’angolo di anti-lift è utile per definire la rotazione attorno all’asse y. Infatti, si può pensare che il gruppo ruota subisca una rotazione ![]()
![]()
![]()

In questo modo si ottiene un altro gradiente cinematico
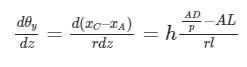
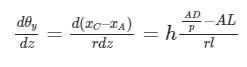
dove si sono indicati con h l’altezza del baricentro, con AD e AL le percentuali di anti-dive e anti-lift, con r il raggio della ruota, con p la ripartizione di frenata e l il passo del veicolo.
Campanatura
Con campanatura si intende l’angolo formato tra la mezzeria verticale del veicolo e dello pneumatico. E’ positivo se le ruote, viste frontalmente, puntano verso l’esterno dell’auto, mentre negativo nel caso opposto. Una campanatura positiva riduce il raggio a terra tra centro ruota e asse di sospensione e quindi facilita la sterzatura, mentre un valore negativo migliora le prestazioni in curva della vettura ed è quindi preferibile nelle auto sportive.
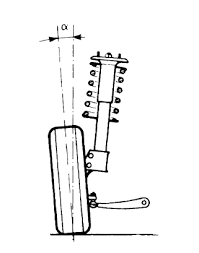

La campanatura, o camber, è legata alle rotazioni lungo l’asse x della vettura. Supponendo di avere uno pneumatico libero, come in figura successiva, se lo si fa traslare verso l’alto questo rimane parallelo a se stesso, ma subisce una rotazione γ’ nel riferimento dell’autovettura.
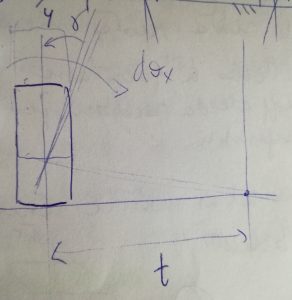

Questa condizione è quella corrispondente ad un totale recupero di camber, ma non è praticamente mai realizzabile né desiderabile. Si ricava allora che, detta CC (camber compensation) la percentuale di variazione di camber desiderata, vale la relazione
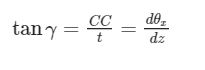
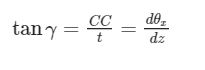
E ora?
Una volta che il comportamento della sospensione è completamente definito, si può passare a posizionare l’asse di sospensione. Questo sarà però oggetto del prossimo articolo.
Riferimenti
- Lezioni di Meccanica del Veicolo, Politecnico di Torino
- Thomas D. Gillespie, Fundamentals of Vehicle Dynamics, cap. 7 Sospensioni