L’analisi limite applicata alla cupola del Taj Mahal
Fin dall’antichità l’arco e la cupola in muratura hanno svolto un ruolo principale nelle costruzioni e ad oggi costituiscono gran parte del patrimonio culturale mondiale.
Sebbene una comprensione statica del funzionamento dell’arco e della cupola si cominci ad avere solamente in epoca romana, sono numerosi i casi di strutture ad arco costruite 6000 anni fa. Lo storico Vitruvio infatti riporta nel suo celebre De Architectura, come un pilastro d’angolo necessitava di uno spessore maggiore, affinché potesse assorbire la spinta esercitata dall’arco. Al tempo, perciò, era già chiaro il funzionamento dell’arco come struttura spingente.
L’analisi limite
L’analisi limite si basa su tre principi semplici quanto efficaci:
-resistenza della muratura nulla
-resistenza a compressione infinita (così come la rigidezza del materiale)
-assenza di scorrimenti tra i blocchi murari
La prima ipotesi è ragionevole, considerando sia la ridotta resistenza a trazione della muratura sia l’eventuale presenza di malta, che presenterà un progressivo peggioramento delle caratteristiche meccaniche nel tempo. Nel caso di muratura a secco risulta naturalmente verificata, almeno nelle sezioni dei giunti.
L’ipotesi di infinita resistenza a compressione della muratura, sebbene sia lontana dalla realtà, risulta accettabile. Generalmente le compressioni agenti sulle singole sezioni sono notevolmente inferiori alla resistenza del materiale.
L’ultima ipotesi formulata da Heyman si basa sull’idea che lo stato tensionale sulla singola sezione del giunto sia quasi esclusivamente di compressione. Nel caso di stereotomia normale (cioè quando I giunti tra I blocchi sono perpendicolari all’asse dell’arco) questa ipotesi è generalmente verificata, mentre ipotizzando una stereotomia differente allora lo scorrimento può dover essere verificato.
La curva delle pressioni
Per comprendere i teoremi dell’analisi limite applicati ad archi e cupole in muratura, è necessario definire la curva delle pressioni. Questa è infatti la curva ottenuta considerando il punto di applicazione delle compressioni sulla sezione di stereotomia, sezione per sezione.
Il teorema statico
Il Safe Theorem, introdotto da Heyman, afferma che:
“se è possibile trovare una curva delle pressioni in equilibrio con i carichi esterni e che giace all’interno della muratura, allora la struttura non collasserà.”
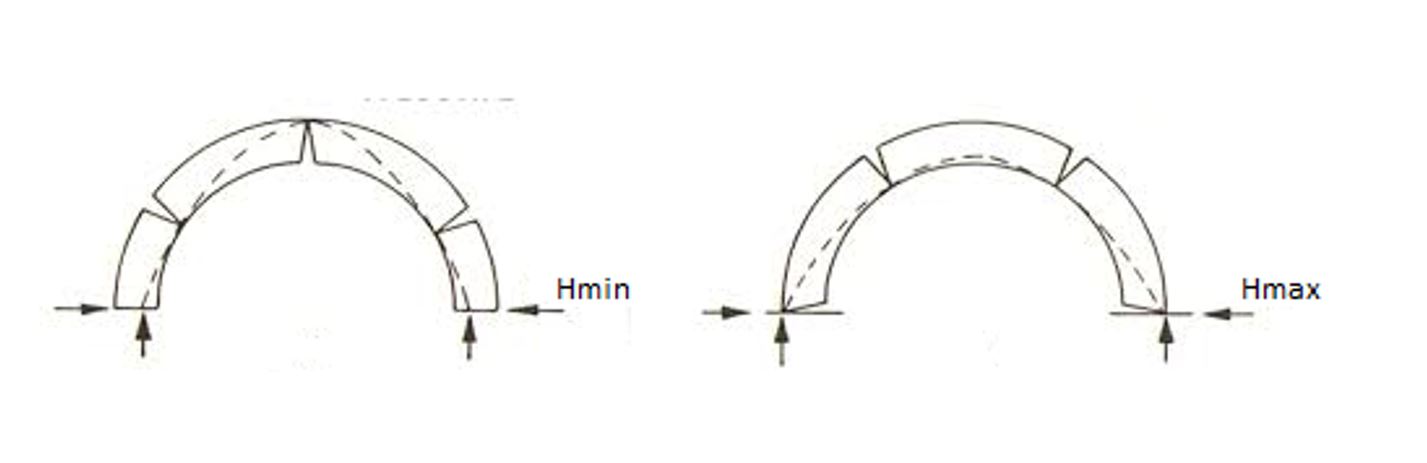
Spinta massima e minima
Il Safe Theorem fornisce inoltre uno strumento pratico, in quanto permette di verificare qualsiasi struttura in muratura attraverso una semplice analisi grafica, senza la necessità di conoscere l’attuale stato di sollecitazione della struttura.
Nell’enunciare il Safe Theorem infatti Heyman presupponeva una condizione di stabilità, condizionata dalla geometria dell’arco. Il tracciamento di una sola curva delle pressioni interna allo spessore dell’arco era una condizione sufficiente per garantire la stabilità dello stesso.
Al fine di trovare la spinta minima, quella massima ed il moltiplicatore orizzontale dei carichi di uno stesso arco bisognerà però arrivare ad una condizione limite, in cui la curva delle pressioni è tangente all’arco, e forma un numero di cerniere tali da sviluppare un meccanismo.
Il teorema statico garantisce che un moltiplicatore dei carichi staticamente ammissibile, cioè rispettoso dell’equilibrio, sia sempre minore del moltiplicatore critico di collasso che quindi ne descrive la condizione limite. Considerato invece uno stato di cedimento, si può verificare come la condizione limite staticamente ammissibile porti alla spinta minima come dimostrato dal prof. Mario Como.
Il teorema cinematico
Il teorema cinematico invece delinea le condizioni di collasso delle strutture in muratura, in quanto afferma che se è possibile trovare un meccanismo rispettoso dei vincoli e per cui i carichi esterni compiano un lavoro positivo allora il moltiplicatore dei carichi esterni sarà sicuramente maggiore o uguale al moltiplicatore critico di collasso.
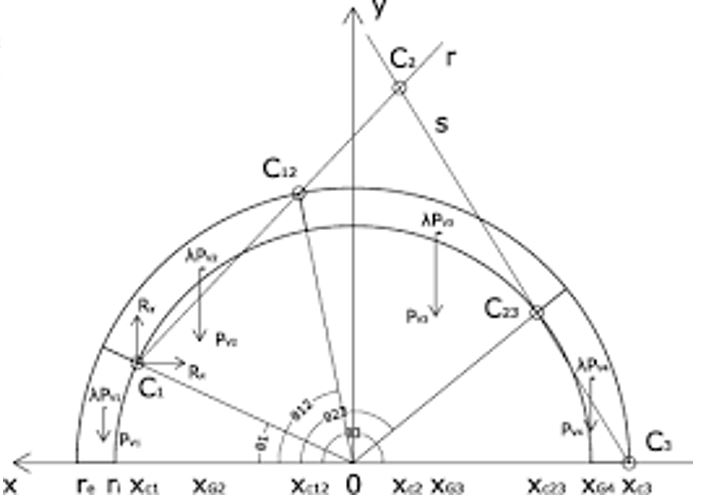
Applicazione del teorema cinematico
L’utilizzo pratico di questo teorema porta però a trovare un moltiplicatore che sovrastima la reale capacità di una struttura. Attraverso un’analisi numerica però si può trovare il minimo di questi moltiplicatori, andando a descrivere esattamente il meccanismo di collasso, e trovando perciò la condizione limite.
Il moltiplicatore critico di collasso sarà dunque unico e corrisponderà al minorante dei moltiplicatori cinematicamente ammissibile e al maggiorante di quelli staticamente ammissibili. Analogamente al caso del teorema statico, considerando una condizione di cedimento delle imposte, la spinta relativa al collasso sarà la massima tra quelle cinematicamente ammissibili.
Analisi limite del Taj Mahal
Il Taj Mahal può essere considerato uno dei simboli architettonici dell’India. Questo mausoleo fu completato nel 1653 e la sua cupola, alta circa 35 metri, può essere definita il suo tratto distintivo, che l’ha resa famosa nei secoli. La sua forma, che riprende l’architettura islamica, consiste in una curva policentrica che si assesta su un tamburo verticale alto circa 7 metri.
Tutte queste caratteristiche rendono questa struttura di fondamentale importanza per l’architettura mondiale. Non meno importante però é l’aspetto strutturale. La cupola di marmo, infatti é spessa circa 3.5m, al fine di resistere al peso proprio e alle azioni orizzontali del vento a cui é sottoposta. Al fine di analizzare dal punto di vista statico la cupola, perciò, ci si può avvalere dei teoremi dell’analisi limite per le strutture in muratura. In questo studio si è utilizzato il teorema statico, attraverso un’implementazione dello stesso in un programma MATLAB a cura del Prof. Ing. Paolo Bisegna e del Prof. Ing. Nicola Nodargi dell’università di Tor Vergata.
La geometria relativa alla cupola del Taj Mahal è molto particolare. E’ stata perciò ripresa da un articolo della rivista scientifica Current Science, che fornisce un rilievo dettagliato dell’estradosso della cupola centrale. Lo spessore della cupola è costante e pari a 3.96m.
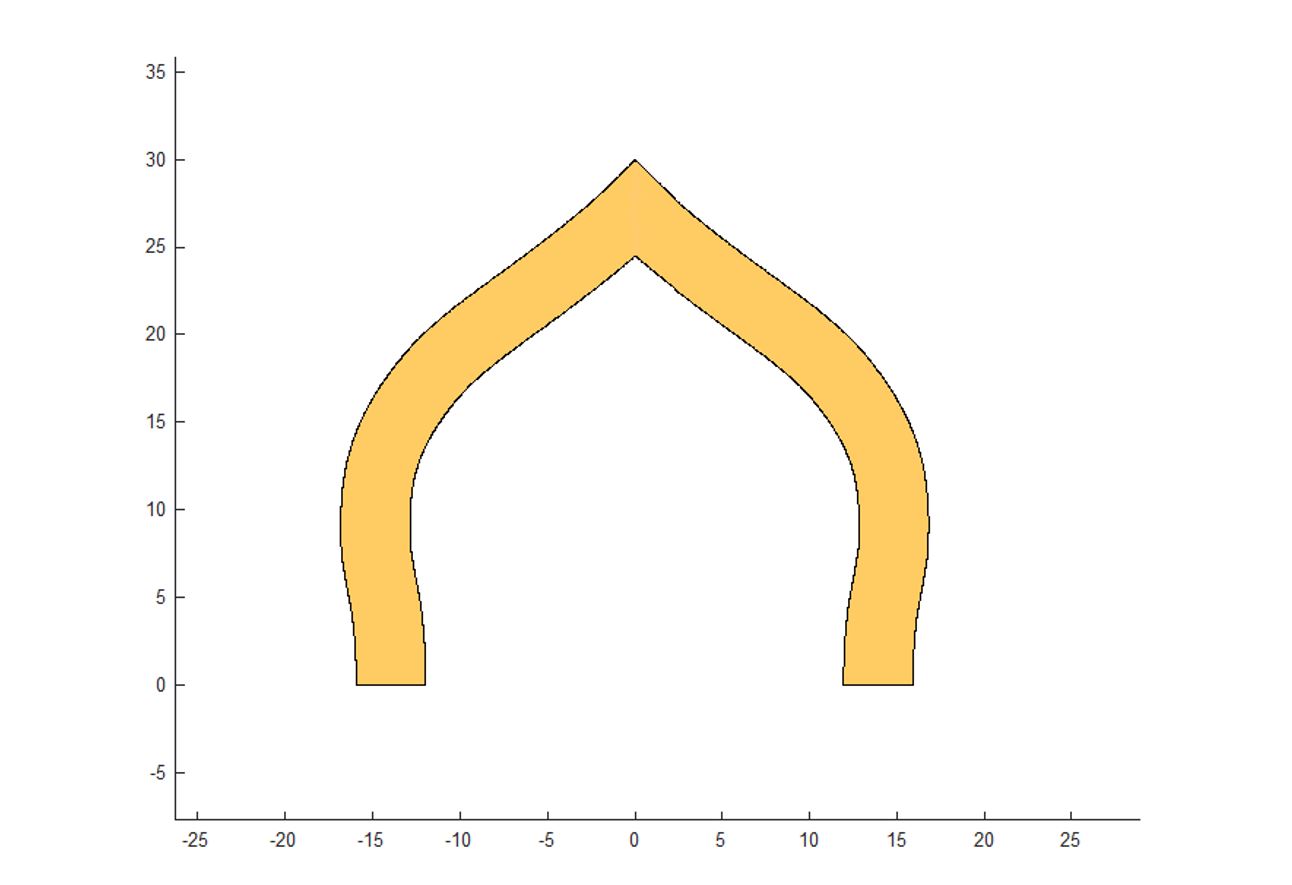
Geometria della cupola del Taj Mahal
La spinta minima che si ricava dallo studio è di 1931.77 kN per unità di angolo ϑ. Rapportando la spinta al peso proprio la spinta normalizzata è pari a 0.0696 un valore molto basso sicuramente riconducibile al rapporto f(freccia)/L(luce) molto grande ma soprattutto allo spessore della cupola.
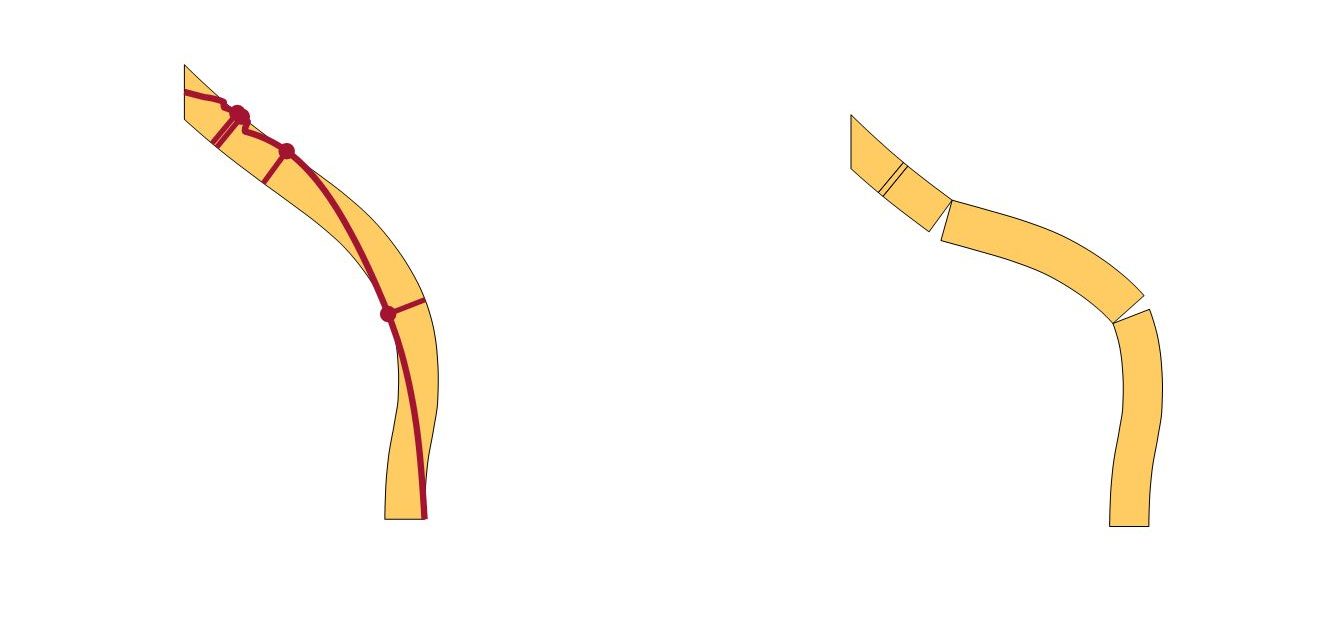
Curva delle pressioni e Meccanismo di collasso
In ogni caso si può notare come una cupola di dimensioni così imponenti possa risultare relativamente poco spingente tramite una geometria prettamente sviluppata in verticale (il rapporto f/L della cupola del Taj Mahal è pari a 1.88).
Si può perciò concludere che l’analisi limite sia un potente mezzo che permette di garantire la sicurezza di strutture in muratura. I teoremi sono inoltre facilmente implementabili in codici di calcolo che permettono un analisi rapida ed efficace.
Fonti
- M. V. Pollione, De Architectura, vol. VI, Pordenone: Edizione Studio Tesi, 1990, p. 291
- J. Heyman, Equilibrium of shell structures, Oxford: Clarendon Press, 1977
- J. Heyman, The Stone Skeleton – Structural Engineering of Masonry Structures, Cambridge: Cambridge university Press, 1985
- N. A. Nodargi e P. Bisegna, Thrust line analysis revisited and applied to optimization of masonry arches, International Journal of Mechanical Sciences, 2020
- M. Como, Minimum and Maximum thrust states in statics of ancient masonry bridges, Rotterdam: Sinopoli, 1998.
- M. Ashkan e A. Yahaya, Persian Domes: History, Morphology and Typologies, Archnet-IJar, International Journal of Architectural Design, 2009.
- D. R. Ahuja e R. Mandyam, On the symmetry of the central dome of the Taj Mahal, vol. 110, Current Science, 2016, pp. 996-999.