Arte Con Un Computer (Parte 1)
Questo articolo tratta il problema dello “Style Transfer”, ossia si cercherà di rispondere alla domanda: “Può un computer, partendo da un’opera d’arte e una fotografia, realizzare un’ interpretazione di quest’ultima utilizzando lo stesso stile del pittore dell’opera d’arte?”
La risposta a questa domanda è affermativa, e si ottengono risultati più che soddisfacenti.
Oggi questo è possibile grazie alle reti neurali convoluzionali, ossia un tipo di reti neurali in cui la connettività tra i neuroni è ispirata all’organizzazione della corteccia visiva animale.
Questo progetto ha preso più di uno spunto dal paper “A Neural Algorithm of Artistic Style” di Leon A. Gatys redatto nell’agosto del 2015.
Si cercherà, in questa sede, di avere il più possibile una filosofia bottom-up: si partirà dalla teoria che è presente dietro questo tipo di realizzazioni, discutendo del suddetto paper e degli strumenti matematici che sono alla base di queste realizzazioni; si giungerà infine all’implementazione software del progetto in esame.
Le implementazioni sono scritte in Python, utilizzando oltre al core di quest’ultimo anche altre librerie scientifiche e specifiche per i progetti di reti neurali. Si sfrutteranno due modelli di rete neurale convoluzionale: VGG-16 e VGG-19, che saranno descritti nel dettaglio nel corso dell’articolo.
Introduzione
L’obiettivo di questo progetto è quello di permettere ad un computer di realizzare un’opera d’arte partendo esclusivamente da una fotografia e dal quadro di un pittore.
L’immagine che sarà il risultato dell’algoritmo che andremo ad implementare più avanti dovrà avvicinarsi il più possibile al contenuto della fotografia ed avvicinarsi il più possibile allo stile adottato dal pittore nella determinata opera d’arte che forniremo in input.
Un altro obiettivo che andrà di pari passo a quello appena descritto, sarà quello di rendere il più possibile facile la comprensione di questo report al lettore che si appresterà a leggerlo, fornendo e spiegando inizialmente le basi teoriche e matematiche dietro questo progetto.
Perchè questa scelta? Questa è la mia massima forma d’arte…
Ho deciso di approfondire questa tematica per un semplice motivo: fin da piccolo, sono sempre stato interessato alla pittura e al disegno in generale, ma nonostante i miei tentativi sia scolastici sia individuali, non riuscivo ad andare oltre la composizione di un omino stilizzato. Tra l’altro riuscivo a disegnare male anche quest’ultimo:
Al contrario credo di essere un fotografo decente.
Nella mia vita ho sempre cercato di ovviare ai miei limiti tecnici grazie all’ausilio della macchina che amo di più usare al mondo: il computer. La domanda che mi è quindi sorta spontanea nel corso degli anni è stata: “È possibile unire informatica e fotografia per generare un qualcosa che si avvicini il più possibile all’arte pittorica?”
Dopo aver seguito il corso di Metodi Quantitativi per l’Informatica all’Università di Roma “La Sapienza” ed essere venuto a conoscenza del Deep Learning ho potuto rispondere in maniera affermativa a questa domanda.
Ciò mi ha permesso di creare, in un periodo di tempo ragionevole, delle opere d’arte, anche se queste non provenivano in effetti direttamente dalla mia mano.
Le implementazioni che vedremo successivamente, sono del tipo CPU-friendly in quanto al momento non dispongo di una scheda video dotata di tecnologia CUDA.
Una scheda video di questa tipologia accorcia in maniera tangibile il tempo d’esecuzione dell’algoritmo, permettendo la realizzazione di immagini con una risoluzione maggiore.
CUDA è una tecnologia hardware sviluppata da Nvidia che rende possibile il calcolo parallelo sulle GPU, aumentando esponenzialmente le prestazioni.
Il Paper di Leon A. Gatys
Il progetto è stato ispirato dal paper di Gatys, Ecker e Bethdge, chiamato: “A Neural Algorithm of Artistic Style” e redatto nel 2015.
Il paper presenta un algoritmo per “trasportare” appunto, lo stile di un autore, da un quadro di sua creazione ad un’altra immagine, come ad esempio una fotografia.
Questo algoritmo permette quindi di mettere il calcolatore in condizioni tali da poter effettuare delle vere e proprie opere d’arte.
Questo è possibile grazie a dei modelli di reti neurali convoluzionali (che d’ora in avanti abbrevieremo con CNN, dall’inglese “Convolutional Neural Network”), chiamate reti-VGG e sviluppate da un team dell’Università di Oxford.
Per ottenere una rappresentazione dello stile dell’immagine, verrà utilizzato un feature space che avrà lo scopo iniziale di contenere l’informazione sulla texture dell’immagine.
Un feature space infatti è una struttura dati n-dimensionale contenente le variabili descrittive dell’immagine.
Stiamo parlando dell’immagine di stile che viene fornita in input, quindi dell’opera d’arte. Non vogliamo estrarne il suo contenuto, ma solo lo stile appunto che la caratterizza. Questo metodo ci permette di ottenere una rappresentazione di quest’ultimo, in maniera tale che non sia possibile in alcun modo risalire al contenuto dell’opera pittorica.
Per ottenere il nostro scopo, la manipolazione delle due immagini (quella rappresentante lo stile e quella rappresentante il contenuto desiderati), deve essere effettuata in maniera indipendente l’una dall’altra.
Successivamente, ad ogni iterazione dell’algoritmo, verrà creata una nuova immagine che al suo interno cercherà di essere il più vicino possibile all’immagine contenuto, per quanto riguarda la disposizione degli elementi, e all’immagine stile per quanto riguarda la colorazione, la tecnica della pennellata, ecc.
Naturalmente, ad ogni ciclo, l’obiettivo sarà quello di ottenere un risultato migliore del precedente che si allontani il meno possibile dalle immagini date in input secondo le suddette caratteristiche.
Ottenere un risultato che soddisfi perfettamente entrambi i requisiti non è chiaramente possibile.
Si giungerà comunque ad un’immagine finale più che soddisfacente grazie all’implementazione di funzioni che terranno in considerazione la perdita di stile e di contenuto in modo da poter minimizzare il più possibile questi due valori.
Le Reti VGG
Prima di procedere è necessario precisare che le reti VGG sono state progettare per la classificazione di immagini, e sono tra le più famose nonchè tra le più efficienti per quanto riguarda la computer vision.
Per ricongiungerci al lavoro che viene qui presentato, è inoltre di grande importanza il fatto che sono state utilizzate in altri progetti per il riconoscimento del periodo di realizzazione di diverse opere artistiche.
Nel paper di Leon A. Gatys e soci si fa esclusivamente riferimento alla rete VGG-19, che è a tutti gli effetti la rete più complessa del gruppo delle VGG.
Nell’implementazione dell’algoritmo verranno fornite due versioni, una sfrutterà VGG-16 (leggermente meno complessa) e una VGG-19. Infine, verranno confrontati i risultati delle due implementazioni.
La versione realizzata con VGG-16, darà anch’essa risultati soddisfacenti e con tempi di esecuzione minori della versione VGG-19. Sembra comunque che quest’ultima abbia sempre una marcia in più rispetto alla sorella minore in termini di risultato complessivo.
Per la sintesi delle immagini, gli autori del paper preferiscono utilizzare l’average pooling al posto del max pooling affermando di ottenere dei risultati leggermente migliori. In questa sede, come scelta progettuale, verranno sfruttati gli strati max_pooling delle reti, in quanto dopo aver revisionato i risultati delle due implementazioni, non si sono trovate differenze tali da rendere più complessa la realizzazione del problema in esame.
Vengono quindi mostrate le due architetture VGG-16 e VGG-19:
| VGG-16 | VGG-19 |
| Immagine Input | Immagine Input |
| 2 Strati Convoluzionali + ReLU | 2 Strati Convoluzionali + ReLU |
| Strato Max Pooling | Strato Max Pooling |
| 2 Strati Convoluzionali + ReLU | 2 Strati Convoluzionali + ReLU |
| Strato Max Pooling | Strato Max Pooling |
| 3 Strati Convoluzionali + ReLU | 4 Strati Convoluzionali + ReLU |
| Strato Max Pooling | Strato Max Pooling |
| 3 Strati Convoluzionali + ReLU | 4 Strati Convoluzionali + ReLU |
| Strato Max Pooling | Strato Max Pooling |
| 3 Strati Convoluzionali + ReLU | 4 Strati Convoluzionali + ReLU |
| Strato Max Pooling | Strato Max Pooling |
| 3 Strati Fully-Connected + ReLU | 3 Strati Fully-Connected + ReLU |
| Strato SoftMax | Strato SoftMax |
Si procede alla descrizione dei diversi livelli che compongono una rete convoluzionale:
STRATO CONVOLUZIONALE: Lo strato convoluzionale è il nucleo centrale di una CNN. I parametri del livello consistono in un insieme di filtri (o kernel) apprendibili, che hanno un campo ricettivo ridotto, ma si estendono attraverso la profondità completa del volume di input.
Durante il passaggio in avanti, ciascun filtro viene convogliato attraverso la larghezza e l’altezza del volume di ingresso, calcolando il prodotto punto tra le entrate del filtro e l’input e producendo una mappa di attivazione bidimensionale di quel filtro. Di conseguenza, la rete acquisisce i filtri che si attivano quando rileva un tipo specifico di feature in una posizione spaziale nell’input.
L’impilamento delle mappe di attivazione per tutti i filtri lungo la dimensione della profondità forma l’intero volume di uscita del livello di convoluzione. Ogni entry nel volume di output può quindi essere interpretata anche come un output di un neurone che osserva una piccola regione nell’input e condivide i parametri con i neuroni nella stessa mappa di attivazione.
STRATO RELU: ReLU è l’abbreviazione di Rectified Linear Units. Questo livello applica la funzione di attivazione non saturata f(x) = max(0, x). Aumenta le proprietà non lineari della funzione decisionale e della rete globale senza influenzare i campi ricettivi dello strato di convoluzione.
Altre funzioni sono usate anche per aumentare la non linearità, per esempio la tangente iperbolica saturante f(x) = tanh(x), f(x) = abs(tanh(x)) e la funzione sigmoide f(x) = (1+e^(-x))^(-1). ReLU allena la rete neurale molte volte più velocemente senza una penalty significativa in fase di generalizzazione.
STRATO MAX POOLING: Divide l’immagine di input in un insieme di rettangoli non sovrapposti e, per ciascuna di tali sottoregioni, calcola il massimo. Sostanzialmente, la posizione esatta di una feature è meno importante della sua posizione rispetto alle altre. Lo strato di pooling serve a ridurre progressivamente la dimensione spaziale della rappresentazione, a ridurre il numero di parametri e la computazione all’interno della rete, e quindi a controllare anche l’overfitting, ossia il sovradattamento a determinate situazioni e caratteristiche.
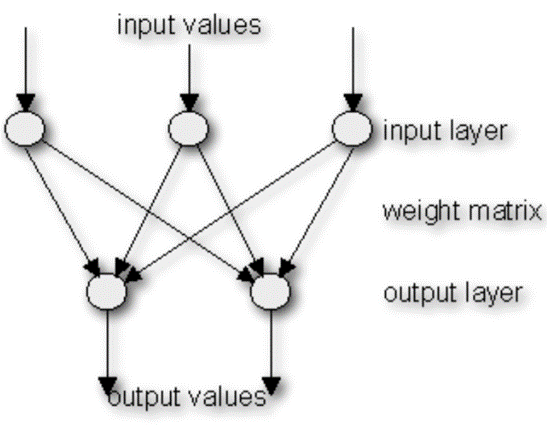
STRATO FULLY CONNECTED: Dopo diversi strati convoluzionali e max pooling, il “ragionamento” di alto livello nella rete neurale viene effettuato tramite strati completamente connessi. I neuroni in uno strato completamente connesso hanno connessioni a tutte le attivazioni nel livello precedente, come si vede nelle normali reti neurali animali. Le loro attivazioni possono quindi essere calcolate con una moltiplicazione di matrice seguita da una compensazione introdotta dal bias.
STRATO SOFTMAX: è uno strato di perdita, specifica in che modo l’allenamento penalizza la deviazione tra le etichette previste e quelle attese ed è normalmente il livello finale.
La Softmax viene utilizzata per prevedere una singola classe di K classi mutuamente esclusive.
Per questa volta abbiamo messo abbastanza carne al fuoco. Restate sintonizzati la prossima settimana per la parte matematica e implementativa dove inizieremo a sporcarci veramente le mani.
Se avete domande potete contattarmi all’indirizzo [email protected]