Arte Con Un Computer (Parte 2)

La scorsa settimana abbiamo steso la prima infarinatura sui problemi riguardanti lo Style Transfer (ossia il fenomeno di trasferire lo stile di un artista in una fotografia) e sulle reti neurali (in particolare quelle della classe VGG).

Il discorso introduttivo della scorsa volta lascerà adesso il posto ad un altro di natura più scientifica e implementativa: inizieremo infatti con l’introduzione dei modelli matematici utilizzati per raggiungere il nostro obiettivo ed arriveremo a mostrare le tecnologie software ed hardware che sono servite sempre a tale scopo.

Iniziamo quindi con…

Un po’ di matematica

Dato uno strato [latex]l[/latex], siano:

• [latex]N^{i}[/latex] numero di filtri, ognuno con la sua feature map;
• [latex]M^{l}[/latex] dimensioni della feature map [latex]h \times w[/latex];
• [latex]F^{l}\in R^{N^{l}\times M^{l}}[/latex] matrice delle risposte dello strato;
• [latex]F_{ij}^{l}[/latex] attivazione dell'[latex]i[/latex]-esimo filtro nella posizione [latex]j[/latex];
• [latex]P^{l}[/latex] matrice rappresentante l’immagine originale;
• [latex]\vec{p}[/latex] immagine originale;
• [latex]\vec{x}[/latex] immagine processata.

Per quanto riguarda il contenuto, il nostro obiettivo è quello di eseguire la discesa del gradiente su un’immagine contenente, all’inizio, esclusivamente del rumore bianco, per trovare un’altra immagine che si avvicini alle feature dell’immagine originale.

La discesa dei gradiente è un algoritmo di ottimizzazione iterativa per trovare il minimo di una funzione. Per trovare un minimo locale di una funzione utilizzando la discesa del gradiente, si eseguono passi proporzionali al negativo del gradiente della funzione nel punto corrente. Se invece uno prende passi proporzionali al positivo del gradiente, ci si avvicina al massimo locale di quella funzione; la procedura è quindi conosciuta come salita del gradiente.

Il nostro scopo è quello di utilizzare la discesa del gradiente anzichè la salita perchè il nostro obiettivo è quello di minimizzare le funzioni di perdita del contenuto e di perdita dello stile. È necessario perciò definire la perdita che l’immagine generata ha in confronto a quella originale come l’errore quadratico medio delle loro due rappresentazioni:

[latex]L_{content}(\vec{p},\vec{x},l) = \frac{1}{2} \sum\limits_{ij} (F_{ij}^{l} – P_{ij}^{l})^{2}[/latex]

La derivata della perdita rispetto alle attivazioni [latex]\frac{\partial L_{content}}{\partial F_{ij}^{l}}[/latex] dello strato [latex]l[/latex] è pari a:

[latex] \begin{cases}(F^{l}-p^{l})_{ij} \hspace{0.2cm} se \hspace{0.2cm} F_{ij}^{l}>0\\0 \hspace{0.2cm} se \hspace{0.2cm} F_{ij}^{l}<0\end{cases}[/latex]

da cui il gradiente rispetto all’immagine generata può essere calcolato usando lo standard error della back-propagation.

Possiamo quindi modificare questa immagine fino a quando non generi la stessa risposta dell’immagine originale nei diversi strati della rete che selezioneremo in fase di implementazione. Per quanto riguarda lo stile, ricordiamo che dobbiamo costruire, su ogni strato della rete, una rappresentazione di esso che computi le correlazioni tra le diverse risposte al filtro.

Al fine di ottenere queste correlazioni tra feature, useremo uno strumento matematico chiamato Matrice di Gram. Nell’algebra lineare, una matrice Gram di un insieme di vettori [latex]v_{1}, …, v_{n}[/latex] è la matrice hermitiana dei prodotti interni, i cui valori sono dati da [latex]G_{ij}=<v_{i},v{j}>[/latex]. In matematica, una matrice Hermitiana (o matrice autoaggiunta) è una matrice quadrata complessa che è uguale alla sua trasposta coniugata, cioè, l’elemento nella riga [latex]i[/latex]-esima e la colonna [latex]j[/latex]-esima è uguale al complesso coniugato dell’elemento nella riga [latex]j[/latex]-esima e nella [latex]i[/latex]-esima colonna, per tutti gli indici [latex]i[/latex] e [latex]j[/latex]. Le matrici hermitiane possono essere intese come l’estensione complessa di matrici simmetriche reali.

Per ottenere una matrice Gram, moltiplicheremo la matrice [latex]F[/latex] rappresentante la risposta al filtro, per la sua trasposta.

[latex]G_{ij}^{l} = \sum\limits_{k} F_{ik}^{l} F_{jk}^{l}[/latex]

Come prima, tramite la discesa del gradiente, partiamo da un’immagine contenente rumore bianco, per avvicinarci il più possibile a quella che contiene al suo interno la rappresentazione dello stile desiderato.

Il rumore bianco è un segnale casuale di uguale intensità a diverse frequenze, che gli conferisce una densità spettrale di potenza costante. Il termine è usato, con questo o altri significati, in molte discipline scientifiche e tecniche, tra cui fisica, ingegneria del suono, telecomunicazioni, previsioni statistiche e molti altri. Il rumore bianco si riferisce a un modello statistico per segnali e sorgenti di segnale, piuttosto che a un segnale specifico. Il rumore bianco prende il nome dalla luce bianca.

Si ha:

[latex]E_{l} = \frac{1}{4N_{l}^{2}M_{l}^{2}} \sum\limits_{i,j} (G_{ij}^{l} – A_{ij}^{l})^{2}[/latex]
[latex]L_{style} (\vec{a},\vec{x}) = \sum\limits_{l=0}^{L} w_{l}E_{l}[/latex]

Dove [latex]w_{l}[/latex] è il peso che viene assegnato al determinato strato.

La derivata tra il contributo della perdita totale in stile di un determinato strato [latex]l[/latex] rispetto alle attivazioni del medesimo [latex]\frac{\partial E_{l}}{\partial F_{ij}^{l}}[/latex] è pari a:

[latex]\begin{cases}\frac{1}{N_{l}^{2}M_{l}^{2}} ((F^{l})^{T}(G^{l}-A^{l}))_{ji} \hspace{0.2cm} se \hspace{0.2cm} F_{ij}^{l}>0\\ 0 \hspace{0.2cm} se \hspace{0.2cm} F_{ij}^{l}<0\end{cases}[/latex]

I gradienti del contributo in perdita di stile dello strato rispetto alle attivazioni degli strati inferiori vengono calcolati, anche qui, utilizzando lo standard error della back-propagation.

Si giunge, infine, ad una funzione rappresentante la perdita complessiva in termini di contenuto e di stile. Il nostro obiettivo sarà chiaramente quello di minimizzare la seguente funzione:

[latex]L_{total}(\vec{p},\vec{a},\vec{x}) = \alpha L_{content}(\vec{p},\vec{x}) + \beta L_{style}(\vec{a},\vec{x})[/latex]

dove [latex]\alpha[/latex] e [latex]\beta[/latex] sono i pesi che assegniamo rispettivamente ai valori di perdita di contenuto e di stile calcolati tramite le suddette funzioni.

L’implementazione

Siamo giunti al fatidico momento dell’implementazione vera e propria dell’algoritmo di Style Transfer.

Come precedentemente accennato, verranno fornite due versioni di questa implementazione, una basata su VGG-16 e una su VGG-19.

È possibile reperire il codice integrale del progetto presso questo link.

Di seguito vengono riepilogate le tecnologie adottate:

CONFIGURAZIONE CALCOLATORE:
– PROCESSORE: Intel Core i5-3350 @ 3.30 GHz x 4
– SISTEMA OPERATIVO: Windows 10 (VGG-16) e Linux Mint 18.3 (VGG-19)
– Kernel Linux (VGG-19): 4.13.0-31
– Memoria RAM: 16GB
– Altri componenti omessi dalla descrizione in quanto non inerenti al problema in esame.

LINGUAGGIO DI PROGRAMMAZIONE: Python.

FRAMEWORK: Tensorflow (VGG-16) e PyTorch (VGG-19).

FORMATO: ipynb, ossia iPython Notebook visualizzabile con Jupyter Notebook.

LIBRERIE AGGIUNTIVE: Jupyter, PIL, Numpy, Matplotlib, Pygame, Clint.

A sua volta, ogni versione contiene altre due sottoversioni, in modo che l’utente possa decidere se lasciar lavorare l’algoritmo per una certa quantità di tempo o farlo smettere solo quando si è giunti ad un livello soddisfacente di convergenza del valore della funzione di perdita che verrà sempre deciso dall’utente finale.

Per decidere quale delle due versioni avviare sarà necessario commentare e decommentare le relative porzioni di codice. In entrambi i casi, si sconsiglia, in un ambiente CPU-friendly l’elaborazione di immagini di risoluzione superiore a 512×512. Se si è in possesso di una scheda video dotata di tecnologia CUDA è possibile andare oltre i limiti di risoluzione consigliati. La versione VGG-19 è già CUDA-ready, mentre per quella VGG-16 sarà necessario installare il pacchetto tensorflow-gpu sul proprio calcolatore. Per ottenere prestazioni ancora superiori, sarà necessario installare quest’ultimo pacchetto compilandolo direttamente dal codice sorgente. Le istruzioni sono all’interno di questo link.

La versione VGG-19 sarà dotata di un algoritmo di ottimizzazione chiamato L-BFGS che utilizza un quantitativo di RAM limitato in fase di esecuzione e che solitamente dà risultati ancora più soddisfacenti della classica discesa del gradiente. Questa scelta, in confronto a VGG-16 è giustificata dalla semplicità di aggiunta di questo ottimizzatore grazie al framework PyTorch, la cosa non è altrettanto vera per quanto riguarda Tensorflow.

Vengono infine forniti maggiori dettagli sulle librerie utilizzate:

JUPYTER: Jupyter Notebook è un’applicazione Web open source che consente di creare e condividere documenti che contengono codice in tempo reale, equazioni, visualizzazioni e testo narrativo. Gli utilizzi includono: pulizia e trasformazione dei dati, simulazione numerica, modellazione statistica, visualizzazione dei dati e molto altro.

PIL: è la libreria di Python che permette la manipolazione delle immagini.

NUMPY: è il pacchetto fondamentale per il calcolo scientifico con Python.

MATPLOTLIB: è una libreria per il plotting bidimensionale che fornisce rappresentazioni dati di qualità in una varietà di formati e ambienti interattivi su piattaforme diverse.

PYGAME: libreria per la realizzazione di giochi in Python, nel progetto viene utilizzata per avvertire l’utente quando l’algoritmo termina il suo lavoro tramite la riproduzione di un file audio.

CLINT: libreria utilizzata per creare una progress bar durante il download del modello VGG-16. Per avere una spiegazione più dettagliata dell’implementazione, si rimanda alla lettura dei Jupyter Notebook contenenti il codice stesso.

Per avere una spiegazione più dettagliata dell’implementazione, si rimanda alla lettura dei Jupyter Notebook contenenti il codice stesso.

Alcuni esempi con VGG-16

Contenuto: Fotografia di Polignano a Mare

Stile: The Angel Standing in the Sun, William Turner

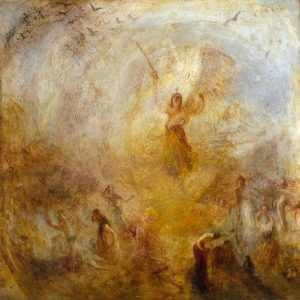
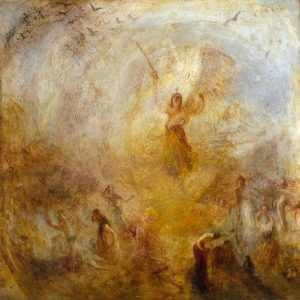
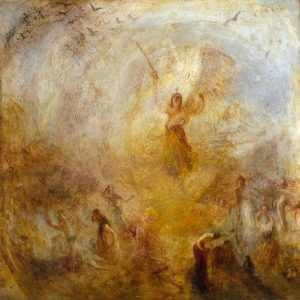
Risultato

Contenuto: Fotografia di Erika

Stile: La Notte Stellata, Vincent Van Gogh

Risultato

Alcuni esempi con VGG-19

Contenuto: Fotografia di Polignano a Mare

Stile: The Angel Standing in the Sun, William Turner

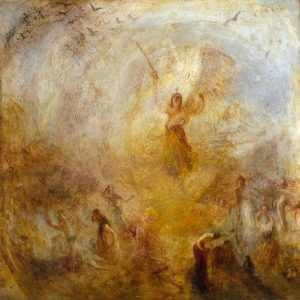
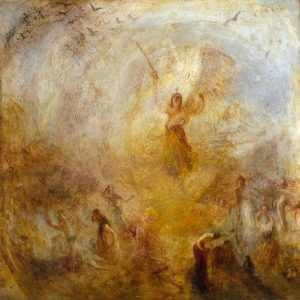
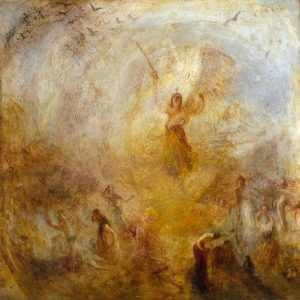
Risultato

Contenuto: Fotografia di Erika

Stile: La Notte Stellata, Vincent Van Gogh

Risultato

Conclusioni

Per concludere, si può dedurre che il quesito in copertina: “Può un computer produrre arte?”, ha sicuramente una risposta positiva.

Nello Style Transfer il calcolatore trasferisce lo stile di un’artista in un’altra immagine, ma la domanda che è naturale porci è: “Potrà un computer generare il suo stile personale e produrre opere d’arte senza emulare nessun altro artista?”

Visti i grandi passi avanti che sono stati fatti nella computer vision e nel Deep Learning in generale è possibile immaginare che anche questa domanda potrà avere un giorno una risposta affermativa e chissà, magari questo futuro non è neanche così lontano.

Alla stesura di questo paper sono presenti altri modelli di rete neurale convoluzionale che non sono stati utilizzati e affrontati in questa sede. Alcuni sono molto “giovani” e molti altri modelli verranno sicuramente realizzati nei prossimi anni. VGG-16 e VGG-19 sono molto complesse e richiedono una potenza di calcolo non indifferente, è probabile che tra qui a qualche anno sarà possibile ottenere lo stesso risultato se non migliore, con reti di gran lunga più efficienti in termini di risorse.

Bibliografia

Si consiglia la lettura dei seguenti libri:

– Machine Learning: A Probabilistic Perspective, di Kevin P. Murphy
– Hands-On Machine Learning With Scikit-Learn and Tensorflow, di Aurelien Geron

Ringraziamenti

Si ringrazia la professoressa Fiora Pirri e il professor Francesco Puja dell’Università di Roma “La Sapienza” per avermi fornito le conoscenze adatte a poter realizzare questo progetto nell’ambito del corso di Metodi Quantitativi per l’Informatica del dipartimento di Ingegneria Informatica, Automatica e Gestionale Antonio Ruberti, e di aver sempre colmato ogni dubbio in merito a questo progetto che sempre mi ha entusiasmato fin dai suoi primi giorni di vita.

Sono sempre pronto a rispondere alle vostre domande all’indirizzo [email protected]

Emanuele Fabi

Laureato in Ingegneria Informatica all'Università di Roma "La Sapienza", da sempre appassionato di motori e sport motoristici.