Orientiamoci! Determinare l’orientamento di un oggetto (parte 2)
Nel precedente articolo abbiamo spiegato le basi teoriche per la determinazione dell’orientamento di un oggetto tramite la conoscenza degli angoli ξ, η e ζ. In questa seconda parte vedremo come leggere e sfruttare “nella realtà” le informazioni necessarie a ricavarli.
Elaborazione e problematiche
In accordo a quanto dimostrato nella prima parte, non si possono ricavare con precisione gli angoli di Eulero dal solo giroscopio. Il motivo principale per cui questo avviene è che non si può determinare l’angolo ζ. Mentre gli altri due angoli prendono come riferimento la direzione della forza di gravità, che viene rilevata dall’accelerometro (comunemente questa direzione viene detta “verso il basso” e allineata con l’asse z fisso), i soli giroscopio e accelerometro non danno nessun riferimento per il calcolo dell’angolo z, ad esempio il nord.
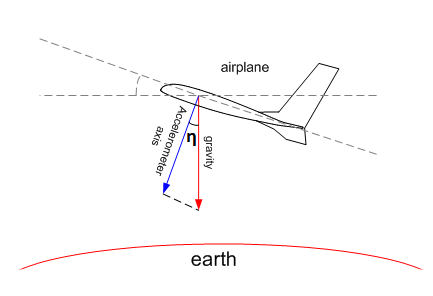
Il disallineamento permette di giungere all’angolo. Sul piano dell’aereo non ci sono però riferimenti.
E’ quindi necessario aggiungere un altro riferimento e la soluzione naturale risulta essere un magnetometro, uno strumento che è in grado di rilevare il campo magnetico terrestre, ovvero una delle direzioni cardinali (per comodità abbiamo assunto il nord, inteso come polo nord magnetico), permettendo così di creare il riferimento per il calcolo dell’angolo z.
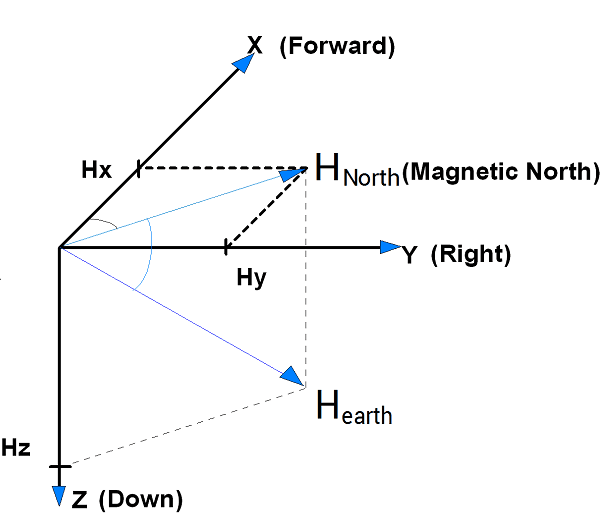
Riferimento nel piano x-y (il nord).
Ma tutto questo perché è necessario?
La ragione è dovuta all’instabilità, inaffidabilità dei tre componenti presi separatamente. Ognuno di essi è affetto da un certo errore dovuto all’una o all’altra causa, che spiegheremo brevemente.
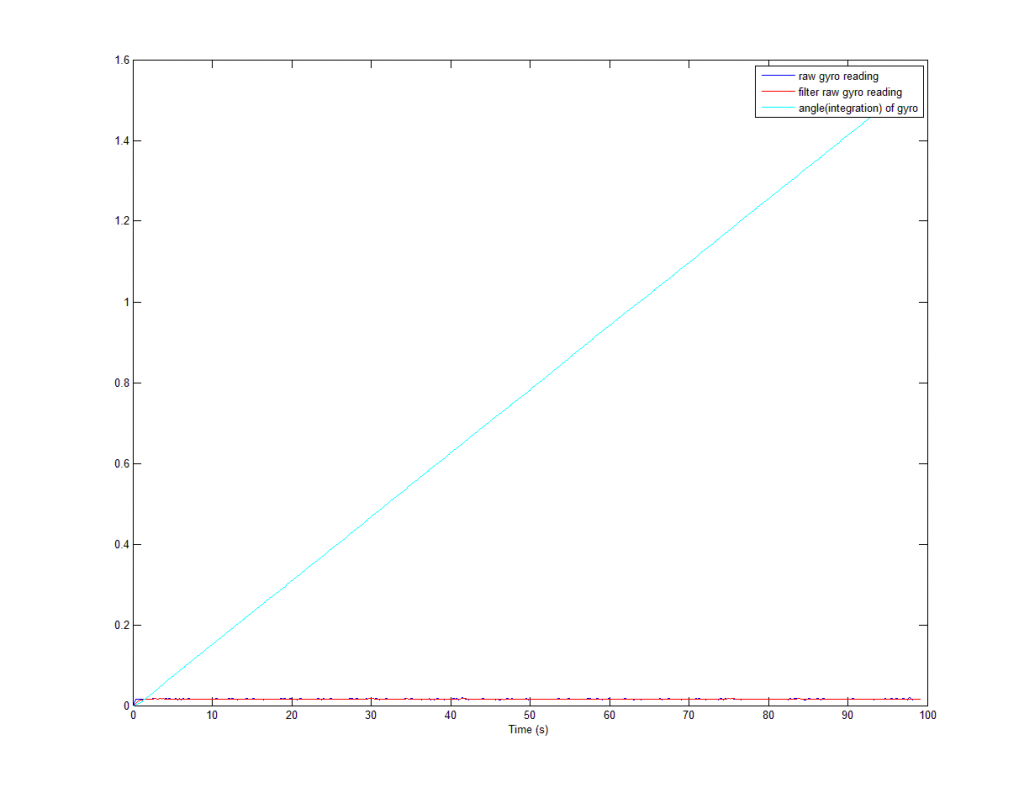
Deriva (qui resa particolarmente evidente) del segnale proveniente dal giroscopio, anche se questo è fermo.
Il giroscopio è affetto da deriva, che è l’accumularsi dell’errore sul segnale acquisito con lo scorrere del tempo. Questo tempo, sui giroscopi a basso costo che vengono messi in commercio (come quello mostrato dopo), è purtroppo molto breve: dopo pochi secondi si accumula un errore paragonabile con i segnali che si vogliono acquisire. Dopo molto tempo si possono quindi ottenere dei risultati completamente distanti dalla realtà.
L’accelerometro è invece affetto da rumore, il sovrapporsi di frequenze “spurie” a quelle rilevate dal segnale. Queste frequenze vanno a provocare delle rapide oscillazioni nella lettura del segnale che però non si accumulano nel tempo.
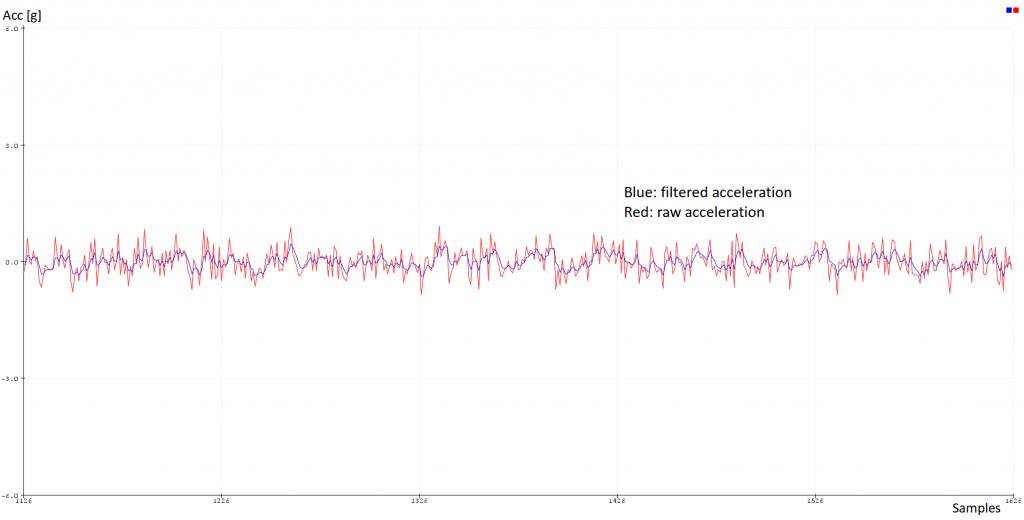
Confronto tra segnale affetto da rumore (rosso) e segnale parzialmente filtrato (blu).
Il magnetometro ha invece una certa dipendenza dalla temperatura, che però per alcune applicazioni è trascurabile; il problema principale di questi componenti è la vicinanza a parti in ferro o acciaio, materiali che provocano una distorsione del campo magnetico e quindi delle letture.
Per risolvere questi problemi, una prima operazione da compiere è quella fondamentale della calibrazione; per saperne di più cliccate su questo link.
Considerando che il giroscopio dà errore su tempi lunghi, l’accelerometro su tempi molto brevi e il magnetometro non è affetto da errori dipendenti dal tempo, è possibile pensare ad una procedura che combini i segnali di questi tre componenti per garantire la stabilità dell’output richiesto, cioè gli angoli di Cardano.
Un’operazione di questo tipo viene detta sensor fusion o sensor fusing cioè la “fusione” (propriamente combinazione) di segnali provenienti da diversi sensori ma correlabili tra loro. La combinazione di questi segnali avviene tramite l’applicazione di particolari filtri predittivi o ricorsivi come il filtro di Kalman. Volendo però mantenere un approccio più familiare si preferisce l’utilizzo di un filtro chiamato filtro complementare che verrà qui spiegato. Per approfondimenti sul filtro di Kalman, si rimanda qui.
Formule
Come dimostrato nel seguente documento è possibile definire gli angoli ξ e η tramite le componenti della gravità rilevate dall’accelerometro. Dalla letteratura inglese, questi vengono denominati angoli di roll e pitch (rollio e beccheggio). Queste sono le rotazioni mostrate in figura.
La loro espressione è:
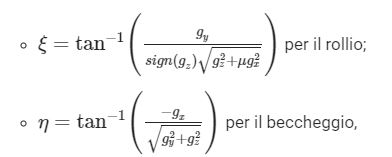
dove g è il segnale di gravità rilevato sul rispettivo asse e μ è un coefficiente correttivo che viene utilizzato per evitare il famigerato Gimbal lock, cioè l’allineamento di uno tra gli assi x e y con l’asse z del corpo con conseguente aumento dei gradi di libertà del sistema e quindi un’indeterminazione di uno degli angoli (per maggiori riferimenti, vedi qui e qui).
Per quanto riguarda l’angolo di yaw (imbardata) o ζ, è il magnetometro a fornire il valore richiesto:
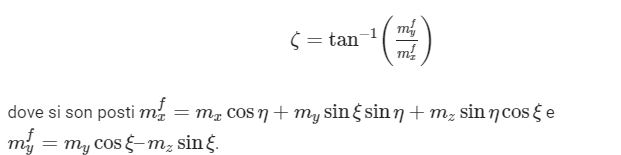
Quest’ultima trasformazione è stata necessaria in quanto il magnetometro è uno strumento che ha un suo orientamento nello spazio, quindi il campo magnetico interseca le varie superfici in maniera sempre diversa e dipendente dall’orientamento dell’oggetto. Le formule sopracitate funzionano quindi alla stessa maniera delle matrici di trasformazione descritte nello scorso articolo, permettendo di esprimere i valori di m{x} e m{y} in un riferimento fisso x-y-z. Per ulteriori approfondimenti cliccate qui.
Filtro complementare
Il filtro complementare può essere assimilato ad un filtro passa basso digitale. Detto s il segnale e i l’istante in cui si rileva il segnale:
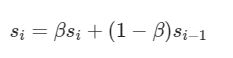
cioè il segnale al tempo corrente è una sorta di media pesata tra il tempo i e i-1 dove il peso è il coefficiente α. L’idea del filtro complementare è quindi di “pesare” il segnale proveniente dal giroscopio con quello proveniente dall’accelerometro/magnetometro. Detti quindi:

possiamo ricavare, tramite integrazione discreta con metodo di Eulero dei segnali del giroscopio e filtro complementare
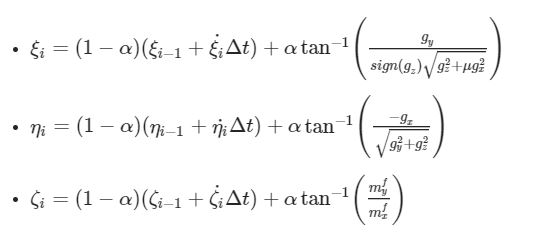
dove α è ricavabile dopo una serie di prove di tuning degli strumenti o tramite programmazione per cercare il valore ottimale. E’ in generale un valore diverso per ognuno degli angoli da calcolare.
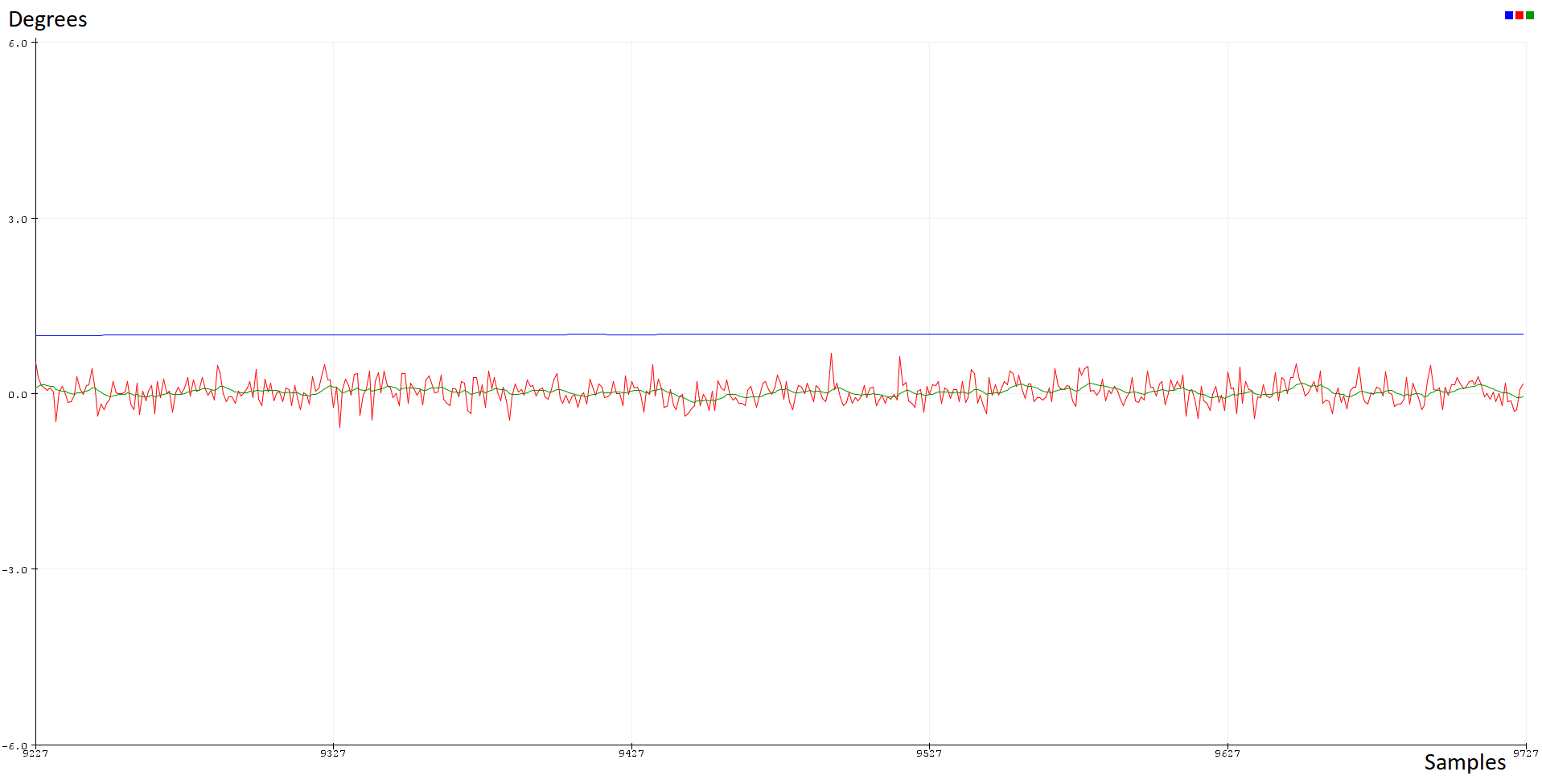
Confronto tra segnale del solo giroscopio (blu), del solo accelerometro (rosso), con il filtro complementare e passa basso applicato (verde) dell’angolo di rollio.
Per ottenere poi un segnale più pulito possiamo applicare a ciascuno degli angoli un filtro passa basso adottando dei nuovi coefficienti β come peso. Più β si avvicina all’unità, più il segnale sarà affetto da delay, come si vede nella figura sotto.
Considerazioni aggiuntive
Nello scorso articolo è stato fatto un riferimento all’utilizzo dei quaternioni per ricavare l’orientamento. Una soluzione basata su questo insieme di numeri è preferibile per applicazioni di precisione con un’alta stabilità richiesta. Tuttavia la maggiore complessità di utilizzo (non tutti gli accelerometri sono in grado di misurarli e talvolta non è possibile accedere ai registri necessari) e la minore intuitività sul loro significato, ha portato a sviluppare un discorso più familiare per la maggior parte dei lettori. Inoltre, l’utilizzo dei quaternioni, consente di “bypassare” la parte di calibrazione.
Per approfondimenti sui quaternioni si rimanda a questo link.